Los Números también  cumplen reglas 

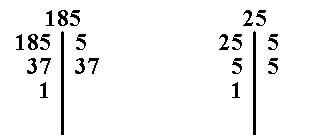
Es tan sencillo el cálculo del m.c.m. que basta que sepas:

Se toman todos los factores que sean diferentes y los que sean iguales, el que tenga el exponente más grande. Si tienen iguales los exponentes, se toma uno de los factores.

En el último ejercicio vemos que tienen el factor 5 los dos números.

En este caso tomamos el de mayor exponente: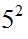 

Factor diferente es el 37.

925 es el número más pequeño que podemos dividir entre 185 y 25 de modo que los cocientes son exactos. El resto vale cero.

3.73 Calcular el número más pequeño al que podemos dividir por 234 y 184, de modo que el resto sea cero:

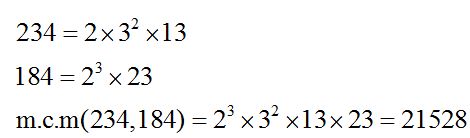
21528 es el número menor que al dividir por 234 y 184 obtenemos un cociente exacto, es decir, el resto vale cero.

3.74 Calcula el número más pequeño que existe que al dividir por 20631 y 3887 los cocientes sean exactos:

Respuesta: 268203

Por si has tenido dificultades:

:

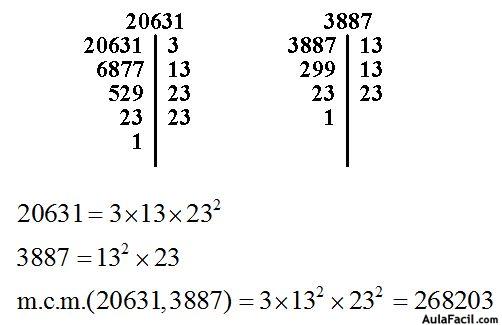
MINIMO COMUN DIVISOR

Explicacion

El Máximo Común Divisor es, como su nombre indica, el mayor de los divisores comunes de varios números. Para calcularlo, se descompone cada uno de ellos en factores primos. El M.C.D. es el resultado de multiplicar los factores que se repitan en todas las descomposiciones, afectados por el menor exponente.

En el caso de que no se repita ningún factor, el M.C.D. de esos números es 1, y se dice que los números son “primos entre sí”. Por ejemplo, el 18 y el 25 son primos entre sí.

Ejemplos:

Si queremos hallar el M.C.D. de 36, 60 y 72, descomponemos los tres en factores primos:

36 = 22·32
60 = 22·3·5
72 = 23·32

Vemos que los únicos factores que se repiten en las tres descomposiciones son el 2 y el 3. Los cogemos con los menores exponentes al que están afectados, por lo que el M.C.D. será 22·3 = 12.

M.C.D.(36, 60, 72) = 12

Para hallar el M.C.D. de 18 y 25:

18 = 2·32
25 = 52

No hay ningún factor repetido, luego:

M.C.D.(18, 25) = 1

Los números 18 y 25 son primos entre sí.

MÍNIMO COMÚN MÚLTIPLO:

El Mínimo Común Múltiplo es, así mismo, el menor de los múltiplos comunes a varios números. Para calcularlo, descomponemos los números en factores primos, y el M.C.M es el resultado de multiplicar los factores comunes y los no comunes, afectados por el mayor exponente.
Si los números son primos entre sí, el M.C.M. es el producto entre ellos.

Ejemplos:

El M.C.M de 36, 60 y 72, que ya tenemos descompuestos más arriba. Los factores que se repiten son el 2 y el 3, y los que no se repiten, el 5. Los cogemos con los mayores exponentes, es decir, 23, 32 y 5. El M.C.M. es, por lo tanto:

M.C.M.(36, 60, 72) = 23·32·5 = 360

El M.C.M. de 18 y 25. Como no se repetía ningún factor, tenemos que cogerlos todos, afectados con el exponente que llevan, es decir, estamos cogiendo todos los factores, por lo que el M.C.M. es el producto de 18·25:

M.C.M.(18, 25) = 2·32·52 = 450